| MODELOVÁNÍ V MECHANICE | OSTRAVA, ÚNOR 2008 |
1 Ing. Petr Frantík, Ph.D., Vysoké učení technické v Brně, Fakulta stavební, Ústav stavební mechaniky, Veveří 331/95, 602 00 Brno, e-mail: kitnarf at centrum dot cz
Abstract
The paper is focused on the results of the numerical simulation of crack propagation during a compression test of a specimen of quasibrittle material. An effective numerical method is used which is based on physical discretisation of the specimen material. The model produces several qualitatively different crack patterns depending on its parameters.
1 Úvod
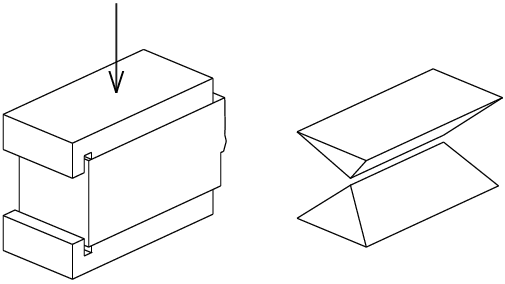
Na Ústavu stavební mechaniky FAST VUT v Brně je dlouhodobě vyvíjena metoda i její implementace pro fyzikální diskretizaci kontinua, viz např. [1,2]. Implementace této metody (v jazyce C a Java) se již dostala do podoby schopné modelovat lomové procesy v kvazikřehkých materiálech. Tento článek se věnuje prvním výsledkům modelování tlakové zkoušky na vzorcích z cementových malt. Jedná se rovněž o volné navázání na článek [3] pojednávající o vlivu okrajových podmínek při modelování tlakové zkoušky. Konkrétně jde o průběh lomového procesu a vznik tlakových/smykových klínů pod ocelovými příložkami zatěžovacího zařízení, viz obr. 1.
Obr. 1: Tlačený vzorek z cementové malty a klínové útvary zbylé po zkoušce
2 Model
Model tlačeného vzorku tvaru je tvořen hmotnými body, které v sobě koncentrují jeho hmotnost. Tyto body na sebe navzájem působí prostřednictvím sítě interakčních pružin s definovanou silovou funkcí. Přístup se podobá netradičním výpočetním metodám, kterými jsou částicové modely a příhradové „lattice“ modely. Vlastnosti interakční funkce souvisí s fyzikálními vlastnostmi materiálu a volbou sítě hmotných bodů a pružin. Pro modelování tlačeného vzorku z cementové malty je vybrána interakční funkce užívaná pro vystižení kvazikřehkých materiálů. Lineární chování je omezeno v tlačené oblasti konstantní hodnotou odpovídající maximální tlakové síle v pružině, viz obr. 2; v tažené oblasti je po dosažení kritického posunutí (resp. maximální tahové síly) použita lineární sestupná závislost až do dosažení nulové hodnoty tahové síly. Poté je pružina považována za přetrženou. Odlehčení probíhá paralelně se vzestupnou větví.
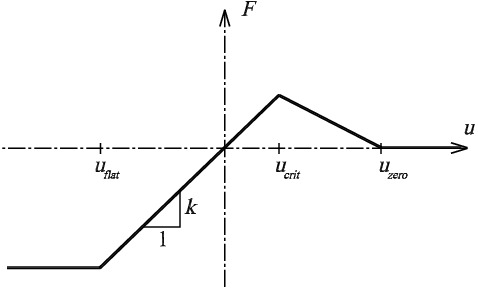
Obr. 2: Použitá interakční funkce (F je síla v pružině, u je protažení pružiny)
Numerický model vzorku je formulován pomocí klasické mechaniky jako nelineární dynamický systém soustavou obyčejných diferenciálních rovnic ve tvaru:
 | (1) |
kde xi a yi jsou souřadnice i-tého hmotného bodu, vxi, vyi jsou složky aktuální rychlosti, Rxi, Ryi jsou složky aktuální výslednice interakčních sil Ri =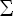 
f(u), kterou pružiny působí na hmotný bod, mi je jeho hmotnost, ci je součinitel útlumu a t je čas. Tato soustava je řešena základními numerickými metodami (Euler, Runge-Kutta).
3 Průběh lomu
Modelován byl homogenní čtvercový vzorek rozdělený na 559 hmotných bodů situovaných do pravidelné, dokonale symetrické „trojúhelníkové“ sítě pružin. Při spodním okraji byl uchycen neposuvně v obou směrech; při horním okraji byl uchycen neposuvně v horizontálním směru, přičemž svislý posuv se měnil konstantní rychlostí. Úloha byla řešena s ohledem na kvalitativní hodnocení průběhu lomu. V závislosti na hodnotách parametrů interakční funkce vznikaly různé obrazce porušení, viz obr. 3 a 4.
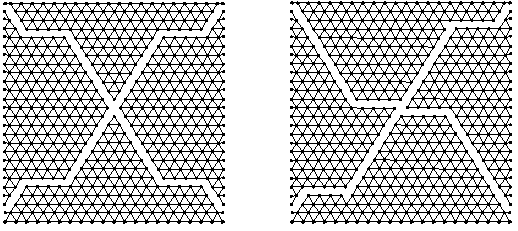
Obr. 3: Charakteristické obrazce porušení modelu při iniciaci ze středu vzorku
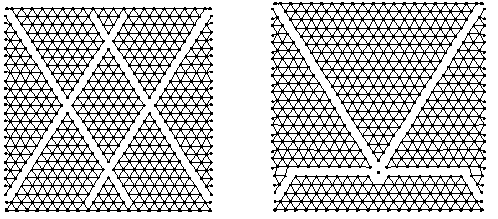
Obr. 4: Charakteristické obrazce porušení modelu při iniciaci z rohu vzorku
Z obrazců porušení je patrné, že dochází k očekávanému formování klínových útvarů, které je do jisté míry dáno i strukturou sítě pružin. Navzdory tomu však model vykazuje překvapivou variabilitu a citlivost na zvolené parametry interakční funkce. U obrazců na obr. 3 se lom inicioval ve středu vzorku; obrazce na obr. 4 odpovídají iniciaci v rozích vzorku.
Iniciace lomu ve středu vzorku
Různé obrazce porušení vzorku byly získány parametrickou studií opřenou o proměnlivost parametrů interakční funkce ucrit, uzero a uflat. Bylo zjištěno, že dosažení iniciace lomu ve středu vzorku je v modelu možné jen v malé podmnožině těchto parametrů.
První podmínkou je dostatečná velikost přetvárné práce nutné k přetržení pružiny, která je dána parametrem uzero. Musí platit uzero > ucrit.
Druhá podmínka omezuje poměr mezi parametry ucrit a uflat. Pokud uzero = 20 ucrit pak musí pro daný model přibližně platit uflat / ucrit = –2 ± 10%.
Pokud tyto podmínky splněny nebyly, pak docházelo k iniciaci lomu z rohů vzorku.
5 Závěr
Příspěvek prezentoval první výsledky modelování lomu tlačeného vzorku pomocí popsané fyzikální diskretizace. Ukázalo se, že model umožňuje dva různé způsoby iniciace lomu: z rohů vzorku a ze středu vzorku. Při lomu se formují očekávané klínové útvary, přičemž se objevila překvapivá bohatost na různé lomové obrazce v závislosti na parametrech modelu. Otázkou zůstává význam geometrie sítě hmotných bodů a pružin.
Poděkování
Tento výsledek byl získán za finančního přispění MŠMT, projekt 1M6840770001, v rámci činnosti výzkumného centra CIDEAS.
Literatura
[1] Frantík, P. DISKRÉTNÍ ŘEŠENÍ VZPĚRU PRUTU, seminář Problémy modelování, VŠB-TU Ostrava, 2002
[2] Frantík, P. SIMULACE ZTRÁTY STABILITY ŠTÍHLÉHO PRUTU PŘI KROUCENÍ, konference Modelování v mechanice 2006, VŠB-TU Ostrava
[3] Frantík, P., Keršner, Z., Štancl P. VLIV OKRAJOVÝCH PODMÍNEK PŘI MODELOVÁNÍ TLAKOVÉ ZKOUŠKY, konference Modelování v mechanice 2005, VŠB-TU Ostrava