Experimental results of free vibration measurement of slender steel cantilever beam and its numerical model is described in the paper. The experiment was focused on investigation of damping effects of slender steel beam with very large displacements (the same order like beam length). Material of the beam is linear elastic upon large displacements due to beam slenderness. Special model of slender cantilever beam is used and described. Beam is divided into a number of rigid segments, connected by hinges with linear rotational springs.
Quadratic approximation (depended on segment angular velocity) of damping effect is able to represent real behaviour of selected problem.
Keywords damping, large displacements, slender cantilever beam, nonlinear dynamical system
Úvod
Při kmitání reálných konstrukcí dochází ke komplexním jevům, které způsobují rozptyl (disipaci) sledované formy kinetické energie konstrukce zejména do jejího okolí. Z těchto jevů uveďme např. zvýšení teploty konstrukce (přeměna kinetické energie konstrukce na kinetickou energii atomů resp. molekul hmoty konstrukce) a odpor prostředí (přeměna kinetické energie konstrukce na kinetickou energii atomů resp. molekul okolního prostředí). Přímé postihnutí všech těchto jevů v modelu konstrukce přináší téměř nezvládnutelnou výpočetní složitost. Naštěstí se ukázalo být vhodné tyto jevy v modelu nahradit umělým rozptylem energie zvaným tlumení.
V tomto příspěvku se zabýváme modelem útlumu velmi štíhlého pružného konzolového nosníku, který kmitá v oblastech velmi velkých deformacích. Model konstrukce i útlumu byl vytvořen pro experimentální výzkum chování dynamicky zatíženého nosníku se zaměřením na nelineární jevy, ke kterým dochází při vývoji kmitání (evoluci) zatížené konstrukce - nelineárního dynamického systému. V evoluci nelineárních dynamických systémů hraje tlumení podstatnou roli, a proto bylo nalezení výstižného modelu rozptylu energie důležitým úkolem.
Útlum konstrukcí je běžně modelován pomocí tzv. viskózního tlumení, které je zastoupeno v matematických modelech členem lineárně závislým na rychlosti (viz např. [1],[2]), což v mnoha případech zjednodušuje řešení úlohy. Obecně je jistě možné rozšířit aproximaci útlumu na polynom libovolného řádu.
Konstrukce
Již v úvodu byla naznačena úloha, pro kterou bylo zapotřebí experimentálně stanovit vlastnosti útlumu a vytvořit jeho model i model samotné konstrukce. Pro výzkum nelineárních projevů dynamického systému byl vybrán svisle situovaný, přímý, velmi štíhlý konzolový nosník z oceli (viz obr. 1), která se v uvažované oblasti přetvoření chová lineárně pružně. Nosník je v jedné své rovině ohybu velmi štíhlý, aby mohlo docházet k velmi velkým posunutím (stejného řádu jako délka nosníku) současně při malých přetvořeních materiálu. Naměřené rozhodující parametry nosníku (vzhledem k jeho velké štíhlosti) jsou následující:
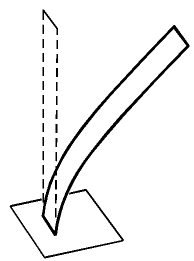
Obr. 1 Znázornění přetvořené konstrukce
Model
Pro numerickou simulaci kmitání vybrané konstrukce byl vytvořen speciální model, jehož konzervativní pohybové rovnice jsou odvozeny v článku [3]. Vzhledem k štíhlosti prutu je výhodné, pro výpočet příčného kmitání, zanedbat smykové přetvoření i konstantní složku normálového přetvoření. Prut je tak možno modelovat ekvidistantním rozdělením na tuhé dílce spojené vzájemně klouby s rotačními pružinami, viz obr. 2.
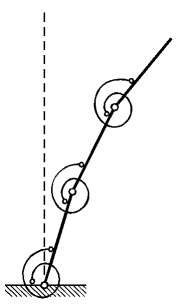
Obr. 2 Model prutu
Tento model lze dle [2] označit jako zvláštní případ metody tuhých fyzických konečných prvků. Díky zanedbání práce normálových a posouvajících sil je eliminován vznik vyšších frekvencí a umožněna větší efektivita numerického řešení.
Pohybové rovnice modelu, včetně tlumících členů, lze zapsat v maticovém tvaru:
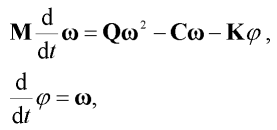 | (1) |
kde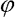 
je vektor pootočení dílců, 
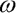je vektor úhlových rychlostí dílců, M je plná symetrická matice momentů setrvačnosti dílců, Q je podobná antimetrická matice, C je diagonální matice útlumu, K je třídiagonální matice tuhosti a t je čas. Matice momentů setrvačnosti M má tvar:
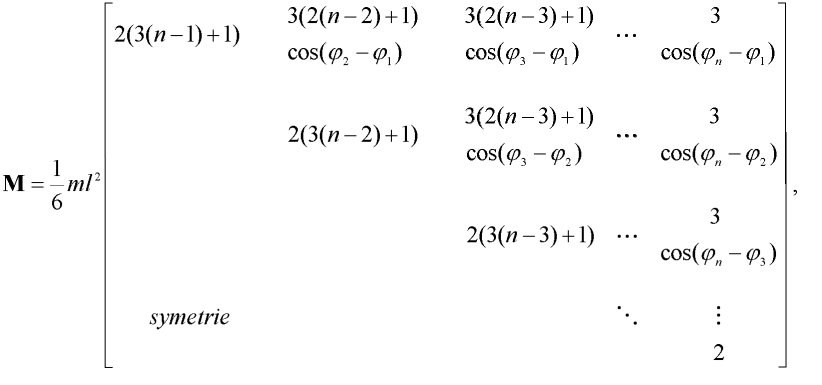 | (2) |
kde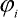 
je pootočení i-tého dílce, vzato vzestupně od dílce u vetknutí prutu, n je počet dílců, l je délka dílce a m je hmotnost dílce. Dále pro matici Q platí:
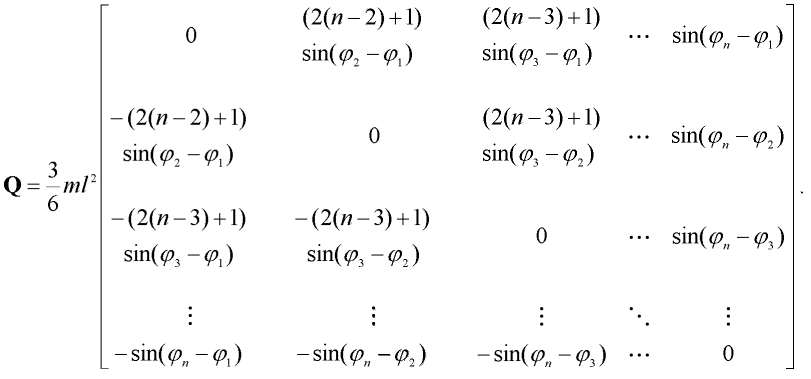 | (3) |
Jestliže k je tuhost rotačních pružin, pro kterou platí k = EI/l, kde EI je ohybová tuhost prutu, pak pro matici tuhosti K platí:
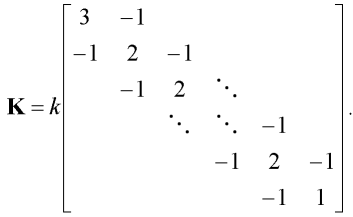 | (4) |
Pro diagonální matici útlumu C můžeme obecně psát:
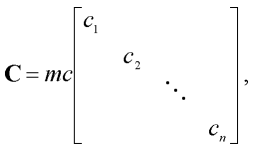 | (5) |
kde c je globální koeficient útlumu a ci je polynom závislý na příslušné úhlové rychlosti 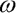i . V případě lineárního (viskózního) útlumu pro studovanou úlohu platí:
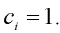 | (6) |
Experiment
Po experimentálním i teoretickém ověření statické i dynamické funkčnosti modelu bylo nutno nastavit vlastnosti teoreticky nejnáročnější součásti numerického modelu - tlumících členů. Prvotním úkolem dynamického experimentálního měření bylo zjistit, zda pro numerické simulace úlohy pro dané podmínky popsané dále, postačuje lineární aproximace útlumu. V negativním případě pak nalézt počet nutných přidaných členů polynomu ci , které je třeba vzít v úvahu (poznamenejme, že předem nebyla vyloučena možnost komplikovanějšího modelu útlumu).
Podmínky experimentu byly zvoleny takové, aby přibližně odpovídaly podmínkám, které měly platit při dynamickém zatěžování. Rozhodující jsou zejména extrémní dosahovaná posunutí a frekvence kmitání prutu. Vzhledem k hledání nelineárních jevů bylo uvažováno se zatěžující frekvencí řádově blízkou dominantní vlastní frekvenci, která byla experimentálně naměřena 2.347 Hz při pozici prutu dle obr. 1. V "základní" pozici, tj. volné kmitání v horizontální rovině, byla změřena vlastní frekvence 2.598 Hz, což odpovídá teoreticky vypočtené hodnotě 2.609 Hz dle [1] (vztah (3.91) na s. 238), která se téměř shoduje s hodnotou 2.606 Hz získanou z modelu s parametry uvedenými výše.
Prut, v pozici dle obr. 1, byl na počátku dostatečně ohnut (pro dosažení velkých posunutí) a poté ponechán volně kmitat. Byl sledován pokles amplitud příčných (tj. horizontálních) výchylek y volného konce nosníku. Výsledek měření je vidět na obrázku 3.
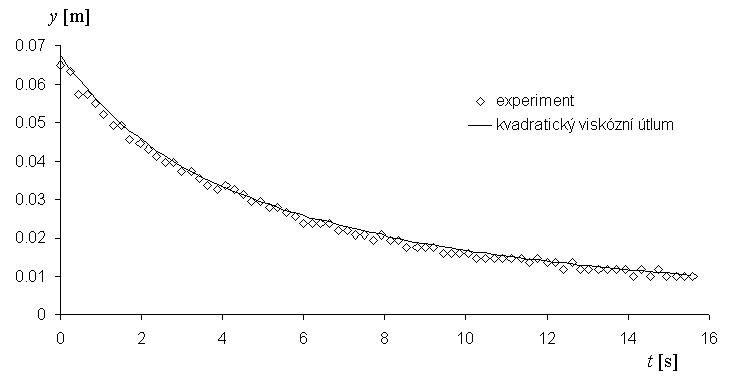
Obr. 3 Srovnání amplitudy příčné výchylky volného konce prutu zjištěné experimentem při volném kmitání s výsledky numerické simulace při užití kvadratického útlumu
Analýzou naměřených amplitud příčné výchylky y bylo zjištěno, že lineární viskózní útlum nevyhovuje. Pokles amplitud nebyl při velkých deformacích exponenciální, jak by odpovídalo lineárnímu útlumu. Proto byla nejprve vyzkoušena kvadratická aproximace ve tvaru:
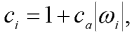 | (7) |
kde ca je relativní koeficient kvadratického člene aproximačního polynomu ci , která při hodnotách:
dala velmi dobrou shodu amplitud (i frekvence) jak je vidět na obrázku 3.
5. Závěr
V příspěvku byl popsán problém nalezení vhodné aproximace reálných tlumících jevů, ke kterým dochází při kmitání jednoduché pružné štíhlé konstrukce v oblastech velkých deformací. Byl popsán úspěšně užitý model úlohy i experiment, s pomocí kterého bylo zjištěno, že pro aproximaci útlumu vybrané konstrukce postačuje aproximace kvadratickým polynomem závislým na úhlové rychlosti dílců modelu.
Lze uvažovat, vzhledem ke známé empirické závislosti odporu vzduchu při obtékání předmětu (která je kvadraticky závislá na rychlosti), že se jedná převážně o tento disipační jev. Tato skutečnost ovšem nebyla prokazována.
Při experimentech bylo také zjištěno, že objemově (ne však hmotnostně) malá přidaná pasivní hmota (závaží na volném konci prutu) neovlivňuje významně kvalitu nalezené aproximace.
Poděkování
Výsledky publikované v tomto článku byly dosaženy při výzkumném pobytu na Bauhaus-Universität Weimar díky projektu Socrates-Erasmus. Zároveň je tento příspěvek součástí výzkumného záměru MSM 261100009 a grantu GA ČR 103/03/1350.
Literatura
Brepta R., Půst L., Turek F. (1994), Mechanické kmitání, Technický průvodce 71, nakladatelství Sobotáles, Praha
Henrych J.: Úplná soustava finitních metod mechaniky a možnosti dalšího rozvoje, studie ČSAV 6.85, nakladatelství Akademia, Praha 1985, 167 stran
Frantík, P., Macur, J.: Diskrétní dynamický model konzoly: Speciální řešení, konference DYN-WIND, TU Žilina, Tále, 2003